Odometrie
Autor: Zbyněk Winkler, 2005-12-05
modely kolových vozidel
Z enkodérů již náš robot může vědět, jak se mu otáčí kolečka. Jak ale tuto informaci
využít k získání určité představy o svém pohybu? Vezmeme si na pomoc odometrii.
Odometrie je proces, který popisuje transformaci dat poskytnutých
enkodéry na změnu pozice a orientace robota. Vlastní slovo odometrie je
složeno ze dvou řeckých slov hodos (cestovat, cesta) a metron (měřit),
což nám napovídá, že se této problematice dostává pozornosti již nějakou dobu
.
Základem odometrie je znalost geometrického modelu robota. Tyto modely se liší
zejména tím, jakých druhů pohybu jsou roboti schopni. Většinu mobilních robotů
můžeme rozdělit do těchto tří kategorií:
- auto
- Kategorie auto zahrnuje roboty, kteří se nedokáží otáčet na místě,
protože změny orientace mohou dosáhnout pouze příslušným natočením
kola či nápravy následovaným pohybem vpřed či vzad. Tomuto způsobu
pohybu se často říká Ackermanovo řízení a zahrnuje většinu dnešních
automobilů.
- tank
- Do kategorie tank patří všichni roboti, co jsou schopni se otáčet na místě
kolem své osy, ale pohybují se pouze vpřed či vzad. Často je nazýváme
diferenciálně řízenými, protože změna orientace závisí na rozdílu rychlosti
levého a pravého kola/pásu.
- všesměroví
- Všesměroví roboti, jak již název napovídá, se dokáží pohybovat
všemi směry bez ohledu na aktuální orientaci, včetně otáčení na místě.
S touto kategorií robotů se nesetkáváme příliš často, i když poslední
dobou začíná být populární v robotickém fotbalu – např. tým
fu-fighters.
Často je nalezneme pod označením omnidrive.
Nyní jednotlivé kategorie popíšeme detailněji.
Auto
Základy modelu pohybu auta si, možná trošku překvapivě, pro
jednoduchost nejprve vysvětlíme na tříkolce. Tříkolka má jedno říditelné
kolečko a dvě pevná, typicky na společné nápravě. Říditelné kolečko určuje
směr pohybu. Tříkolka neumí nezávisle měnit svoji orientaci a pozici a patří
proto do skupiny
nonholonomních robotů.
V závislosti na natočení říditelného kolečka se tříkolka pohybuje bud po přímce
(to když je kolečko rovnoběžně s osou robota) anebo po kružnici. Pro zjištění
změny pozice je třeba dvou údajů – orientace řídícího kolečka a jeho ujetá
vzdálenost. Nechť je referenčním bodem střed nápravy pevných kol. Předpokládáme-li
nenulové natočení řídícího kola, a tedy pohyb po kružnici, bude nás pravděpodobně
zajímat střed a poloměr této kružnice. Jak je vidět z obrázku, střed kružnice
bude ležet na ose pevné nápravy (vlevo, či vpravo podle směru natočení). Poloměr
R je roven
$
R = L ⁄ tan(ω)
kde L$ je vzdálenost náprav a ω úhel natočení. Po této kružnici robot
urazí úhel θ
$
θ = dF⋅cos(ω) ⁄ R
který bude zároveň odpovídat i změně jeho orientace. Změna pozice [dx,dy]
pak bude
dx = R - R⋅cos(θ)
dy = R⋅sin(θ)
$
Pokud by nás zajímala vzdálenost ujetá středem osy pevné nápravy, můžeme
ji vyjádřit za pomoci dF, vzdálenosti ujeté zatáčecím kolem, jako
$
d = dF⋅cos(ω)
$
Pozorování: manévrovací schopnost autíčka závisí na dvou parametrech: jednak je
to vzdálenost mezi osami L (čím kratší tím se snáze zatáčí) a dále jsou to
limitní úhly natočení předního kola. Tyto úhly jsou většinou menší než 90° a
auto se tedy nemůže otočit na místě.
Ackermanovo řízení
Proč jsme se nezabývali hned z počátku klasickým autem, tedy čtyřkolkou?
Důvodem je tzv. Ackermanovo řízení: pokud má být střed otáčení dobře
definován (tj. žádné kolečko nebude ve smyku), tak je nutné, aby vnitřní kolo
zatáčelo více než vnější. Můžeme pak tedy počítat s prostředním „virtuálním
kolem” a dostaneme zmiňovaný model tříkolky.
Tank
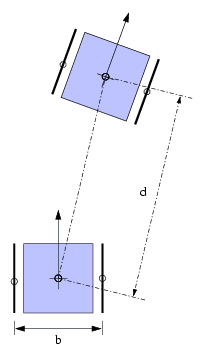
Model diferenciálního robota
|
Dalším modelem, kterému se budeme věnovat, je
tank. Základním rysem
tohoto modelu jsou dvě nezávisle poháněná kola/nápravy. Pokud se obě točí
stejně rychle stejným směrem, robot jede rovně. Pokud se naopak točí opačným
směrem, točí se celý robot na místě kolem středu mezi nápravami. To je také
nejčastější referenční bod.
Pokud je rozdíl rychlostí mezi nápravami nenulový, ale obě nápravy se točí
na stejnou stranu, pohybuje se i tento robot po kružnici. Vzdálenost středu
této kružnice je dána poměrem obou rychlostí:
$
R = ½⋅b⋅(vL + vR) ⁄ (vL - vR)
kde b$ je vzdálenost kol od sebe (rozchod) a vL a vR jsou rychlosti.
Pokud levé kolečko ujede vzdálenost dL a pravé dR změní se orientace
o úhel θ (v radiánech)
$
θ = (dL - dR)/b
$
kde b je již zmiňovaný rozchod. Celková ujetá vzdálenost d (počítaná pro
střed poháněné osy) je pak
$
d = (dL + dR)/2
$
Pozorování: natočení robota závisí pouze na rozdílu celkové ujeté vzdálenosti
pravého a levého kolečka a nikoliv na průběhu jednotlivých změn. K výpočtu
směru tedy stačí i jednoduchý čítač, který lze snadno realizovat i v jednočipu
(nejsou třeba goniometrické funkce).
Všesměroví
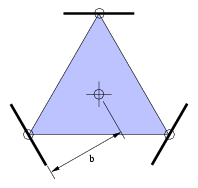
Model všesměrového robota
|
Doposud zmiňované modely byly tzv.
nonholonomní. Vozidlo je
holonomní
pokud počet stupňů volnosti rychlostí odpovídá počtu stupňů volnosti pozice.
Jednoduše řečeno,
holonomní vozidlo může měnit svoji rychlost nezávisle ve
všech směrech. Vznášedlo je příkladem
holonomního vozidla (nic ho neomezuje
ani při pohybu dostran).
Všesměrový podvozek (angl.
omnidirectional
drive) je tedy vlastně speciálním případem obecnějšího konceptu
holonomicity.
Diferenciálně řízení roboti se sice mohou otáčet na místě, ale stále se mohou
pohybovat pouze směrem kolmým k ose kol. Jak tedy dosáhnout schopnosti pohybu
dostrany? Pohybu dostrany brání kola. Co kdybychom obyčejná kola nahradili koly
speciálními, která by místo pneumatiky měla spoustu nezávislých koleček? (tato
kolečka je možné si představit jako nařezanou pneumatiku) Pokud by na robota
byla vyvinuta nějaká vnější síla působící dostrany, nic by nyní pohybu
nebránilo. Vhodnějším uspořádáním kol a zvýšením jejich počtu minimálně na 3
(přece jenom chceme řídit 3 stupně volnosti) dosáhneme požadované
všesměrovosti.
Minimální varianta všesměrového podvozku je na obrázku. Informace potřebné k
výpočtu změny pozice zahrnují jednotlivé enkodéry d1, d2, d3 a vzdálenost kol
od středu robota b.
$
d1 = dx + θ b
d2 = -0.5 dx + 0.867 dy + θ b
d3 = -0.5 dx - 0.867 dy + θ b
$
Odhad pozice
Pokud bychom si chtěli zjednodušit situaci a nepočítat s různými pohyby po
kružnici a podobně, můžeme novou pozici odhadnout. Označíme-li (x, y,
φ) pozici robota, pak odhad nové pozice bude:
$
x = x + dX
y = y + dY
φ = φ + θ
$
V případě nonholonomních robotů můžeme dX a dY vyjádřit pomocí
promítnutí posunu d do globálních souřadnic:
$
dX = d*cos(φ)
dY = d*sin(φ)
$
V případě holonomních robotů do globálních souřadnic promítneme oba lokální
posuny:
$
dX = dx*cos(φ) - dy*sin(φ)
dY = dx*sin(φ) + dy*cos(φ)
$
Tímto způsobem pohyb odhadujeme vždy pohybem po úsečce s následnou
změnou orientace. Tento odhad typicky stačí, protože akumulování změn pozice
stejně nelze použít dlouhodobě. Pokud 8x střídavě robot popojede metr a otočí
se 45 stupňů, tak to bohužel v realitě neznamená, že se dostane zpět na
startovní místo. Malá chyba taky chyba a součet malých chyb = velká chyba,
jinými slovy když robot dlouho pojede pouze pomocí výpočtu relativních změn
pozice, tak tato chyba vždy překročí libovolnou hranici. Není to fatální, ten
metr může ujet docela přesně .
Řešením je použití nějaké
vnější reference, která nám akumulaci chyby
udrží pod kontrolou. Více se o tomto tématu můžete dočíst v kapitole
o
lokalizaci.
Související literatura
Advanced — odometrie s přeurčením parametrů
Jak vylepšit naší odometrii? Co si například počneme, pokud jedno kolečko
podklouzne nebo je volně ve vzduchu? Pokud nemáme absolutní referenci (viz
lokalizace), tak můžeme jenom vylepšovat meření (např. přidáním dalších
enkoderů nebo jiných senzorů). My se nyní zaměříme na případ tříkolky, která má
ale enkodery na všech kolech a zároveň snímá úhel natočení předního kolečka.
Označme si ujeté vzdálenosti jednotlivých kol jako L (left), R (right), F
(front) a úhel natočení předního kola jako A (angle). Pokud je A=0 a my tomuto
faktu zcela věříme, tak jede robot rovně a tedy všechny tři kolečka by se měly
otočit o stejnou vzdálenost, tj. L=R=F. Co dělat, pokud tomu tak není? Máme-li
více měření, tak se typicky buď průměrují nebo se vybírá medián. Pokud např.
došlo k nadzvednutí levého kolečka, tak hodnotě L nemůžeme věřit (může být
větší (?) i menší v závislosti na jeho setrovačnosti (?)). V tomto případě nám
průměr nepomůže a lepší by byl tedy medián. Pokud ale věříme, že alespoň dvě
meření jsou v pořádku, tak můžeme udělat průměr z mediánu a hodnoty jemu
bližší. Příklad pokud L=10, R=32 a F=30, tak medián je F, bližší hodnota je R
a výsledek bude dán jako (R+F)/2=31.
Proberme ještě jeden jednoduchý případ, kdy slepě věříme měření úhlu A. Nechť
robot zatáčí a tedy A<>0. Pak se všechna tři kola pohybují po kružnicích s
různým poloměrem. O jaké poloměry se jedná záleží jednak na hodnotě A, ale také
na parametrech tříkolky (rozchod d a vzdálenost předního kola od zadní osy
l). Poloměry nám zároveň určují očekávaný poměr mezi jednotlivými měřeními.
Pokud je tedy všechny sjednotíme, tedy L/poloměr(L), R/poloměr(R) a
F/poloměr(F), tak můžeme provést stejnou úvahu, jako v předešlém odstavci při
jízdě rovně. Je však dobré mít na mysli ještě jeden detail: pokud jsou enkodery
na všech kolech stejné (což jsme mlčky předpokládali), tak je lepší vzít vážený
průměr — měření nejvzdálenějšího kola bude pravděpodobně nejpřesnější,
protože jeho enkoder natiká nejvíce.
Teď už zbývá „pouze” obecný případ, kdy ani měření úhlu A příliš něvěříme. V
tomto případě je dobré si uvědomit, že z libovolné dvojice parametrů jsme
schopni jednoznačně určit změnu pozice (ano, až na singulární případy, kdy se
robot např. otáčí v místě pravého kolečka (R=0), tak R v kombinaci s A je pro
nás nedostatečné). Můžeme tedy získat 6 nových pozic, ale která je ta správná?
Případně, která odpovídá mediánu? Hrubým přístupem můžeme např. všechny pozice
zprůměrovat, připadně najít mediány v jednotlivých složkách dX, dY, dAngle, ale
je to korektní? Bude výsledek lepší?
Problém nastává pokud je jedno z měření zcela špatně. Pokud budeme používat všech
šest pozic, tak by celá polovička z nich byla špatně. Pokud by dokonce dvě měření
byla nepřesná, tak 5 pozic z 6 bude špatně. Obyčejné průměrování, ale ani medián
jednotlivých složek, nebude fungovat.
Jedno z možných řešení je podobné situaci, kdy jsme věděli, že A=0. V tomto případě
jsme zahodili nejvzdálenější měření a zbylá dvě zprůměrovali. Podobně pro každou
trojici můžeme zjistit chybu a trojici s nejmenší chybou použít jako výsledek.
Pošlete email redakci.
Všechny materiály, které máme k dispozici, jsou již součástí článku, na který reagujete (tj. pokud tam tedy není např. plánek na stavbu, je to proto, že nic takového nemáme).
Vaši zprávu se bohužel nepodařilo odeslat, ale můžete nám napsat sami na adresu webmaster-at-robotika.cz
Vaše zpráva byla úspěšně odeslána
Pro odeslání formulář je třeba mít zapnutý javascript.


